Methoden in Processing: Unterschied zwischen den Versionen
| (7 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 512: | Zeile 512: | ||
x = r * cos(alpha); | x = r * cos(alpha); | ||
| − | y = r * sin(alpha) | + | y = r * sin(alpha); |
Damit können wir jetzt das Programm umsetzen. Wir müssen den Winkel jeweils um einen kleinen Betrag ändern und können so den Weg eines Punktes auf der Kreisbahn verfolgen. | Damit können wir jetzt das Programm umsetzen. Wir müssen den Winkel jeweils um einen kleinen Betrag ändern und können so den Weg eines Punktes auf der Kreisbahn verfolgen. | ||
| Zeile 608: | Zeile 608: | ||
| − | // Zeichnen | + | // Zeichnen der Dreieckslinien |
stroke(255,255,0); | stroke(255,255,0); | ||
line(width/2, height/2, x, y); | line(width/2, height/2, x, y); | ||
| Zeile 619: | Zeile 619: | ||
'''Aufgabe 7''' | '''Aufgabe 7''' | ||
| − | Die Grundidee der Kreisbewegung kann auch für das Erzeugen einer Spirale genutzt werden | + | Die Grundidee der Kreisbewegung kann auch für das Erzeugen einer Spirale genutzt werden. Die Spirale, die durch eine Abfolge von Ellipsen erzeugt wird, soll dabei in einer eigenen Methode erfolgen. |
| Zeile 630: | Zeile 630: | ||
float alpha = radians(0); | float alpha = radians(0); | ||
int c = 255; | int c = 255; | ||
| − | + | ||
| − | + | ||
void setup(){ | void setup(){ | ||
size(500, 500); | size(500, 500); | ||
| Zeile 638: | Zeile 638: | ||
frameRate(200); | frameRate(200); | ||
} | } | ||
| − | + | ||
void draw(){ | void draw(){ | ||
| + | |||
| + | spirale(); | ||
| + | } | ||
| + | |||
| + | void spirale (){ | ||
| + | //Die Spirale wird von einem Punkt beschrieben, der sich auf einer Kreisbahn immer weiter vom Startpunkt (width/2, height/2) entfernt. | ||
| + | |||
float x = r * cos(alpha); | float x = r * cos(alpha); | ||
float y = r * sin(alpha); | float y = r * sin(alpha); | ||
| − | + | ||
noStroke(); | noStroke(); | ||
fill(c); | fill(c); | ||
| − | + | ||
ellipse(width/2 + x , height/2 + y, 16, 16); | ellipse(width/2 + x , height/2 + y, 16, 16); | ||
alpha += 0.01; | alpha += 0.01; | ||
| − | + | ||
//Vergrößerung des Radius um Spiraleffekt zu erzeugen | //Vergrößerung des Radius um Spiraleffekt zu erzeugen | ||
r+=0.05; | r+=0.05; | ||
| Zeile 655: | Zeile 662: | ||
</syntaxhighlight> | </syntaxhighlight> | ||
</popup> | </popup> | ||
| + | |||
| + | |||
| + | [http://www.mathematische-basteleien.de/spirale.htm Anregungen für weitere Spiralen] | ||
| Zeile 672: | Zeile 682: | ||
float alpha = 0.0; | float alpha = 0.0; | ||
float v = 0.05; | float v = 0.05; | ||
| − | float r = | + | float r = 90.0; |
//Faktor, der die Kreisform der äußeren Figur aufhebt | //Faktor, der die Kreisform der äußeren Figur aufhebt | ||
| Zeile 679: | Zeile 689: | ||
void setup(){ | void setup(){ | ||
| − | size( | + | size(400, 400); |
noStroke(); | noStroke(); | ||
} | } | ||
| Zeile 685: | Zeile 695: | ||
void draw(){ | void draw(){ | ||
//Nachzieheffekt durch transparenten Hintergrund | //Nachzieheffekt durch transparenten Hintergrund | ||
| − | fill(0, | + | fill(0, 6); |
rect(0, 0, width, height); | rect(0, 0, width, height); | ||
| Zeile 693: | Zeile 703: | ||
float c = cos(alpha); | float c = cos(alpha); | ||
| − | float x = | + | float x = 200 + (c * r); |
| − | float y = | + | float y = 200 + (s * r); |
//Kleiner "Führungskreis | //Kleiner "Führungskreis | ||
| Zeile 715: | Zeile 725: | ||
</div> | </div> | ||
| + | |||
| + | [https://youtu.be/ggbwa1--sko Weitere Anregungen zum Thema] | ||
Aktuelle Version vom 8. Januar 2017, 17:49 Uhr
Am Ende des Kapitels solltest du
- in der Lage sein, eigene Methoden zu schreiben und an beliebiger Stelle aufzurufen,
- die Namenskonventionen für Methoden kennen,
- die eigenen Methoden mit Hilfe von Parametern flexibel gestalten können,
- in der Lage sein, ein Programm mit Hilfe von Methoden logisch zu strukturieren,
- Kreisbewegungen darstellen können.
Bisher haben wir in allen Aufgaben und Beispielen die vordefinierten Methoden in Processing verwendet. Processing bietet aber auch die Möglichkeit, eigene Methoden zu schreiben und in den Programmen zu verwenden. Dies ist dann interessant, wenn wir dieselbe Anweisungsfolge mehrfach verwenden wollen bzw. in einer Methode mehrere verschiedene Aufgaben unterbringen möchten.
Beginnen wir mit folgendem kleinen Programm:
void setup(){ size(400, 400); background(255); } void draw(){ ellipse(200, 200, 20, 20); }
Wir erstellen nun eine eigene Methode, die das Zeichnen des Kreises übernimmt und bauen sie nach und nach unseren Vorstellungen entsprechend um:
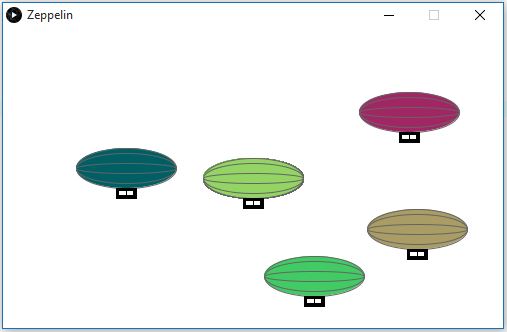
Sehen wir uns noch folgendes, etwas komplexeres Beispiel an, in dem wir auf drei verschiedene Arten Zeppeline auf der Zeichenfläche platzieren können:
float xPos; float yPos; void setup(){ size(500, 300); background(255); } void draw(){ drawZeppelin(width/2, height/2); } void mousePressed(){ drawZeppelin(mouseX, mouseY); } void keyPressed(){ drawZeppelin(random(300)+100, random(100)+100); } void drawZeppelin(float xPos, float yPos){ stroke(100); fill(mouseX-245,mouseY-45, 100); ellipse(xPos, yPos, 100, 40); ellipse(xPos, yPos, 100, 30); ellipse(xPos, yPos, 100, 10); rectMode(CENTER); stroke(0); fill(0); rect(xPos, yPos+25, 20, 10); fill(255); rect(xPos, yPos+25, 15, 5); line(xPos, yPos+22, xPos, yPos+28); } |
Das Beispiel verwendet die selbst verfasste Methode drawZeppelin(). Um Zeppeline an verschiedenen Positionen zeichnen zu können, besitzt die Methode darüberhinaus zwei Parameter, mit denen die Koordinaten des Ankerpunktes der Figur übergeben werden können. Ein Parameter hat die Form Datentyp Bezeichner (z.B. int durchmesser). Mehrere Parameter werden durch Kommas getrennt (z.B. (int x, int y)). In der Methode selbst nutzen wir nur Methoden, die bereits bekannt sind und die auf die Koordinaten des Ankerpunktes zurückgreifen um die komplexe Figur zu zeichnen. Die neue Methode kann nun in den anderen Methoden genutzt werden, indem wir sie über ihren Namen und die entsprechenden Parameterwerte aufrufen.
Hinweis: Um mehrere gleichartige Objekte zu zeichnen, gehen wir wie folgt vor: Wir erstellen eine Figur mit dem Mittelpunkt der Zeichenfläche (width/2, height/2) als Ankerpunkt. Alle anderen notwendigen Koordinaten werden von diesem Punkt ausgehend dargestellt (z.B. width/2 + 20). Ist die Figur fertiggestellt ersetzen wir alle Vorkommen von width/2 durch xPos und alle Vorkommen von height/2 durch yPos. Jetzt müssen wir xPos und xPos nur noch als Parameterwerte der Methode einsetzen und können über den Methodenaufruf die Figur an beliebiger Stelle zeichnen lassen.
Namenskonvention für Methoden
Methoden können wie Variablen beliebige Namen tragen. Aus Lesbarkeitsgründen sollte der Name einer Methode aber ausdrücken, was die Methode leistet (z.B. unsichtbarMachen()). Er sollte daher ein Verb enthalten. Methodennamen werden üblicherweise klein geschrieben. Falls sie aus mehreren Worten bestehen, sollten die Folgeworte mit Großbuchstaben beginnen (z.B. dieBesteMethodeVonAllenAusfuehren()).
Vertiefung: Video-Sequenz zum Thema "Methoden" (engl.)
Aufgabe 1
Folgender Code erstellt auf der Zeichenfläche ein Haus und einen Baum.
void setup(){ size(500, 300); } void draw(){ fill(255); rect(200, 150, 100, 80); fill(255, 0, 0); triangle(200,150,250,120,300,150); fill(0); rect(220, 170, 20, 20); rect(260, 170, 30, 60); fill(82, 49, 15); rect(395, 100, 20, 80); fill(0,255,0); ellipse(405, 70, 60, 80); }
Erstelle in einem ersten Schritt jeweils eine Methode für das Zeichnen des Hauses und des Baums und rufe die beiden Methoden in der draw()-Funktion auf. Verändere anschließend die beiden Methoden mit Hilfe von Parametern so, dass Häuser und Bäume durch Aufruf in der draw()-Funktion an beliebiger Stelle erzeugt werden können.
Die Aufgabe zeigt schön die Vorteile eigener Methoden für Teilaufgaben des Programms: Zum einen wird der Code übersichtlicher, zum anderen können die Teilaufgaben mehrfach ausgeführt und zudem mit Hilfe von Parametern auch noch flexibel gestaltet werden.
Aufgabe 2
Erstelle ein Programm mit dem eine UFO-Armee erzeugt werden kann. Das Zeichnen der Flugobjekte soll in einer eigenen Methode erfolgen.
Aufgabe 3
Erstelle ein Programm, das mit Hilfe von zwei Punkten ein Gitter erzeugt. Für die Bewegung der zwei Punkte soll jeweils eine eigene Methode sorgen.
Aufgabe 4
a) Erstelle ein Programm, bei dem der Aufeinanderprall zweier Kugeln zu einer Explosion führt. Die Explosion wird von einer Methode explode() gesteuert. Für die Darstellung benötigt man ein entsprechendes Bild. Hilfreich sind die Funktionen dist() und noLoop()
b) Ändere das Programm so ab, dass eine Kugel auf der Zeichenfläche umherschießt und beim Aufprall auf eine "Bombe" explodiert. Erstelle dafür drei Methoden für die Darstellung der Kugel (display()), die Bewegung der Kugel (move()) und die Steuerung der Explosion (explode()).
Aufgabe 5
a) Ändere das folgende Programm so ab, dass die Linie in alle Richtungen verlängert werden kann:
int xPos = 200; int yPos = 200; void setup(){ size(400, 400); background(0); } void draw(){ stroke(255, 0, 0); strokeWeight(3); point(xPos, yPos); } void keyPressed(){ if(keyCode == RIGHT){xPos = xPos + 1;}; }
b) Baue nun das Grundprinzip der Tastensteuerung so um, dass man damit einen Ballon steuern kann, der vor Wolken vorbei zieht. Benötigt werden zusätzlich eine Methode zeichneBallon() und eine Methode zeichneWolke().
Exkurs: Bewegung auf der Kreisbahn
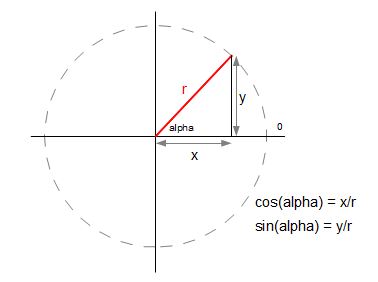
Bisher haben wir nur lineare Bewegungen in Processing simuliert. Wir wollen nun unser Spektrum erweitern und uns Kreisbewegungen zuwenden. Dazu müssen wir auf einige mathematische Vorkenntnisse zurückgreifen. Gehen wir vom bekannten Einheitskreis aus:
Wenn wir die Formeln entsprechend umformen, erhalten wir x- bzw. y-Koordinate des Punktes der sich in Abhängigkeit des Winkels auf der Kreisbahn bewegt:
x = r * cos(alpha);
y = r * sin(alpha);
Damit können wir jetzt das Programm umsetzen. Wir müssen den Winkel jeweils um einen kleinen Betrag ändern und können so den Weg eines Punktes auf der Kreisbahn verfolgen.
float xcenter; // Mittelpunkt auf der x-Achse float ycenter; // Mittelpunkt auf der y-Achse float r = 200; // Radius der Kreisbahn float alpha = 0; // aktueller Rotationswinkel void setup () { size (550, 500); background (220); //Koordinatensystem line(width/2, 0, width/2, height); line(0, height/2, width, height/2); // Rotationsmittelpunkt xcenter = width / 2; ycenter = height / 2; } void draw () { // Veränderung des Rotationswinkels alpha += 0.03; // Berechnung der aktuellen Position float x = xcenter + cos (alpha) * r; float y = ycenter + sin (alpha) * r; // Zeichnen des Kreises stroke(255,0,0); strokeWeight(2); point (x, y); }
Aufgabe 6
Ändere nun das obige Programm so ab, dass ein Dreieck um den Einheitskreis wandert. Lagere dabei das Zeichnen des Koordinatensystems und das Zeichnen des Dreiecks jeweils in eine eigene Methode aus.
Aufgabe 7
Die Grundidee der Kreisbewegung kann auch für das Erzeugen einer Spirale genutzt werden. Die Spirale, die durch eine Abfolge von Ellipsen erzeugt wird, soll dabei in einer eigenen Methode erfolgen.
Anregungen für weitere Spiralen
Einen interessanten Effekt kann man erzielen, indem man die folgenden beiden Zeilen zu Beginn der draw()-Funktion einfügt:
fill(0, 7); rect(0, 0, width, height);
Dadurch wird bei jeder Aktualisierung der draw()-Funktion ein transparentes Rechteck über die Zeichenfläche gelegt, wodurch der Eindruck entsteht, ein Kreis mit Schweif würde die Spirale beschreiben. Dieser Effekt spielt auch bei folgendem Programm eine Rolle:
float alpha = 0.0; float v = 0.05; float r = 90.0; //Faktor, der die Kreisform der äußeren Figur aufhebt float sx = 3.0; float sy = 1.5; void setup(){ size(400, 400); noStroke(); } void draw(){ //Nachzieheffekt durch transparenten Hintergrund fill(0, 6); rect(0, 0, width, height); //Festlegung der Koordinaten des "Führungskreises" alpha += v; float s = sin(alpha); float c = cos(alpha); float x = 200 + (c * r); float y = 200 + (s * r); //Kleiner "Führungskreis fill(255); ellipse(x, y, 1, 1); //Berechnung der äußeren Figur auf der Basis der Koordinaten des inneren Kreises float x2 = x + cos(alpha * sx) * r/2; float y2 = y + sin(alpha * sy) * r/2; ellipse(x2, y2, 6, 6); }
Aufgabe 7
Experimentiere mit den Parametern des obigen Programms um eigene kreative Ergebnisse zu erzielen.