Methoden in JAVA: Unterschied zwischen den Versionen
(→Getter- und Setter-Methoden) |
|||
| (9 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | <div style="background-color:#A9E2F3; padding:10px; margin-bottom:30px;"> | ||
| + | '''Am Ende des Kapitels solltest du''' | ||
| + | * die verschiedenen Arten von Methoden, die wir innerhalb einer Klasse verwenden, unterscheiden können, | ||
| + | * wissen, wie eine Methode mit Rückgabewert aufgebaut ist und funktioniert, | ||
| + | * Getter- und Setter-Methoden erstellen können und ihre Funktion verstehen. | ||
| + | </div> | ||
| + | |||
| + | |||
Wir kennen bereits verschiedene Arten von Methoden. Das folgende Beispiel zeigt sie in der Anwendung: | Wir kennen bereits verschiedene Arten von Methoden. Das folgende Beispiel zeigt sie in der Anwendung: | ||
| Zeile 30: | Zeile 38: | ||
//Methoden mit Parameterwert | //Methoden mit Parameterwert | ||
| − | public void einzahlen(int betrag | + | public void einzahlen(int betrag){ |
kontostand=kontostand+betrag; | kontostand=kontostand+betrag; | ||
} | } | ||
| − | public void auszahlen(int betrag | + | public void auszahlen(int betrag){ |
kontostand=kontostand-betrag; | kontostand=kontostand-betrag; | ||
} | } | ||
| Zeile 156: | Zeile 164: | ||
kilometerstand = kilometerstand + strecke; | kilometerstand = kilometerstand + strecke; | ||
tankinhalt = tankinhalt - strecke*7/100;} | tankinhalt = tankinhalt - strecke*7/100;} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
} | } | ||
} | } | ||
| Zeile 176: | Zeile 178: | ||
Um auch die Wurzel von Zahlen < 1 berechnen zu können wählt man 0 als Untergrenze und 1 als Obergrenze. Die Methode muss für diesen Sonderfall erweitert werden. | Um auch die Wurzel von Zahlen < 1 berechnen zu können wählt man 0 als Untergrenze und 1 als Obergrenze. Die Methode muss für diesen Sonderfall erweitert werden. | ||
| − | Es bietet sich nun noch an, das Ergebnis mit der Berechnung über die entsprechende Methode aus dem Package java.lang.Math zu vergleichen. | + | Es bietet sich nun noch an, das Ergebnis mit der Berechnung über die entsprechende Methode aus dem Package ''java.lang.Math'' zu vergleichen. |
<popup name="Materialien"> | <popup name="Materialien"> | ||
| Zeile 188: | Zeile 190: | ||
<popup name="Lösungshinweise"> | <popup name="Lösungshinweise"> | ||
| − | + | ||
* Die Methode benötigt zwei Eingabewerte, die als Parameter realisiert werden: die Zahl, deren Wurzel gesucht wird und die Genauigkeit, mit der das Ergebnis ermittelt werden soll. | * Die Methode benötigt zwei Eingabewerte, die als Parameter realisiert werden: die Zahl, deren Wurzel gesucht wird und die Genauigkeit, mit der das Ergebnis ermittelt werden soll. | ||
* Es müssen zwei Variablen für die Ober- und die Untergrenze deklariert und initialisiert werden. | * Es müssen zwei Variablen für die Ober- und die Untergrenze deklariert und initialisiert werden. | ||
| Zeile 195: | Zeile 197: | ||
* Zum Schluss gibt man den Wert der Quadratzahl, den die Methode aus java.lang.Math errrechnet aus, um das Ergebnis zu prüfen. | * Zum Schluss gibt man den Wert der Quadratzahl, den die Methode aus java.lang.Math errrechnet aus, um das Ergebnis zu prüfen. | ||
* Es bleibt noch der Sonderfall (zahl<1) übrig. Dazu fügen wir vor der Schleife eine Abfrage ein und legen, falls der Sonderfall zutrifft, die Werte für Ober- und Untergrenze entsprechend fest. | * Es bleibt noch der Sonderfall (zahl<1) übrig. Dazu fügen wir vor der Schleife eine Abfrage ein und legen, falls der Sonderfall zutrifft, die Werte für Ober- und Untergrenze entsprechend fest. | ||
| − | + | ||
</popup> | </popup> | ||
| Zeile 494: | Zeile 496: | ||
<div style="background-color:#BEE599; padding:10px; margin-bottom:30px;"> | <div style="background-color:#BEE599; padding:10px; margin-bottom:30px;"> | ||
'''Aufgabe 9''' | '''Aufgabe 9''' | ||
| + | |||
| + | Ergänze die Klasse ''Auto'' aus '''Aufgabe 3''' um eine Methode '''getTankinhalt()''', die den aktuellen Tankinhalt zurückgibt und sicherstellt, dass nicht mit leerem Tank gefahren wird, bzw. bei einem Tankinhalt von weniger als 10 Litern zum Tanken auffordert. | ||
| + | |||
| + | <popup name="Lösungsvorschlag"> | ||
| + | <syntaxhighlight lang="java"> | ||
| + | |||
| + | public double getTankinhalt(){ | ||
| + | if (tankinhalt<=0){System.out.println("Ohne Benzin läuft ein Auto nicht !!");} | ||
| + | else if (tankinhalt<10){System.out.println("Höchste Zeit um an die Tanke zu fahren !!"); return tankinhalt;} | ||
| + | return tankinhalt; | ||
| + | } | ||
| + | |||
| + | </syntaxhighlight> | ||
| + | </popup> | ||
| + | |||
| + | |||
| + | '''Aufgabe 10''' | ||
Erstelle eine Klasse ''Rechteck'' mit den Attributen ''laenge'' und ''breite''. Neben dem entsprechenden Konstruktor enthält die Klasse Getter- und Setter-Methoden für die beiden Werte. In den Setter-Methoden soll zusätzlich sichergestellt werden, dass die Kantenlänge des Rechtecks den Wert 100 nicht überschreitet. Für den Fall einer Überschreitung wir der Hinweis auf einen unzulässigen Wert ausgegeben. Zusätzlich soll zum Testen eine Methode zur Ausgabe der Werte für ''laenge'' und ''breite'' angelegt werden. | Erstelle eine Klasse ''Rechteck'' mit den Attributen ''laenge'' und ''breite''. Neben dem entsprechenden Konstruktor enthält die Klasse Getter- und Setter-Methoden für die beiden Werte. In den Setter-Methoden soll zusätzlich sichergestellt werden, dass die Kantenlänge des Rechtecks den Wert 100 nicht überschreitet. Für den Fall einer Überschreitung wir der Hinweis auf einen unzulässigen Wert ausgegeben. Zusätzlich soll zum Testen eine Methode zur Ausgabe der Werte für ''laenge'' und ''breite'' angelegt werden. | ||
| Zeile 525: | Zeile 544: | ||
if(b>=100){System.out.println("Unzulaessiger Wert !");}else{ | if(b>=100){System.out.println("Unzulaessiger Wert !");}else{ | ||
breite=b; | breite=b; | ||
| + | } | ||
} | } | ||
public void ausgeben(){ | public void ausgeben(){ | ||
| − | System.out.println("Laenge: "+ | + | System.out.println("Laenge: "+getLaenge()); |
| − | System.out.println("Breite: "+ | + | System.out.println("Breite: "+getBreite()); |
} | } | ||
} | } | ||
</syntaxhighlight> | </syntaxhighlight> | ||
</popup> | </popup> | ||
Aktuelle Version vom 26. April 2018, 10:56 Uhr
Am Ende des Kapitels solltest du
- die verschiedenen Arten von Methoden, die wir innerhalb einer Klasse verwenden, unterscheiden können,
- wissen, wie eine Methode mit Rückgabewert aufgebaut ist und funktioniert,
- Getter- und Setter-Methoden erstellen können und ihre Funktion verstehen.
Wir kennen bereits verschiedene Arten von Methoden. Das folgende Beispiel zeigt sie in der Anwendung:
public class Konto{ //Attribute private String name; private String vorname; private String kontonr; private int kontostand; //Konstruktor(-methode) public Konto(String kontonr, String name, String vorname){ this.kontonr=kontonr; this.name=name; this.vorname=vorname; kontostand=0; } //Methoden ohne Parameterwert public void kontodatenAusgeben(){ System.out.println("Kontonummer: "+kontonr); System.out.println("Name: "+name); System.out.println("Vorname: "+vorname); } //Methoden mit Parameterwert public void einzahlen(int betrag){ kontostand=kontostand+betrag; } public void auszahlen(int betrag){ kontostand=kontostand-betrag; } }
Die Konstruktormethoden dienen dazu, ein neu gebildetes Objekt einer Klasse in einen definierten Anfangszustand zu versetzen. In ihrer einfachsten Form haben Methoden keine Parameter, sondern nur einen Namen. Parameter sind Werte, die an eine Methode übergeben werden, damit diese sie in ihren Berechnungen verwenden kann. Ein Parameter hat die Form Datentyp Bezeichner (z.B. int durchmesser). Mehrere Parameter werden durch Kommas getrennt (z.B. (int x, int y)). Wird eine Methode mit Parameter(n) in BlueJ aufgerufen, erscheint eine Eingabeaufforderung, in der der jeweilige Parameterwert eingegeben werden kann. In diesem Fall können wir uns die Verwendung des Scanners für die Dateneingabe sparen. Neben diesen bereits bekannten Arten von Methoden kann eine Klasse noch weitere Arten enthalten.
Aufgabe 1
Erstelle eine Klasse Kreis, die drei verschiedene Konstruktoren enthält und zwei Methoden mit denen die Größe und die Position des Kreises verändert und der aktuelle Wert ausgegeben werden kann.
Aufgabe 2
Erstelle eine Klasse Schueler, mit der Schueler-Objekte erzeugt werden können, die als Attribute Name, Vorname und Klasse enthalten. Daneben soll eine Methode ausgeben() erstellt werde, die die Daten auf der Konsole ausgibt. Diese Methode kann direkt aus dem Konstruktor heraus aufgerufen werden.
Aufgabe 3
Erstelle eine Klasse Auto mit der Auto-Objekte erzeugt werden können. Die Klasse soll die Attribute Kennzeichen, Typ, Kilometerstand und Tankinhalt enthalten. Neben dem Konstruktor, der einen Neuwagen erzeugen soll, besitzt die Klasse noch zwei Methoden tanken() und fahren(). Die Methode fahren() aktualisiert dabei Kilometerstand und Tankinhalt, wobei von einem mittleren Verbrauch von 7l/100km ausgegangen wird. Es soll dabei auch sichergestellt werden, dass nicht mit leerem Tank gefahren wird. Hinweis: Die verbrauchte Benzinmenge errechnet sich aus (Strecke * Verbrauch in l)/100.
Aufgabe 4
Zu erstellen ist eine Methode quadratwurzelBerechnen, die die Quadratwurzel einer Zahl näherungsweise berechnet.Dabei sollen die gesuchte Zahl und die Genauigkeit, mit der die Wurzel berechnet werden soll (z.B. 0.00000001), als Parameter eingegeben werden.
Als Grundlage der Berechnung soll das Prinzip der Intervallschachtelung benutzt werden:
Die Intervallschachtelung startet mit einem Intervall, welches so groß gewählt werden muss, dass sich das Ergebnis in diesem Intervall befindet. (Für Zahlen größer 1 bieten sich 1 als Untergrenze und die Zahl selbst als Obergrenze an.) Dann teilt man dieses Intervall in der Mitte in zwei Teilintervalle und überlegt sich, in welchem der beiden Teilintervalle das Ergebnis liegen muss. Dann fährt man mit diesem Teilintervall fort und teilt es erneut. Dies wiederholt man nun solange, bis die Obergrenze und die Untergrenze des Intervalls nahe genug beieinander liegen (d.h. die gewünschte Genauigkeit des Ergebnisses erreicht ist). Die Mitte dieses letzten Intervalls gibt man dann als Ergebnis aus.
Um auch die Wurzel von Zahlen < 1 berechnen zu können wählt man 0 als Untergrenze und 1 als Obergrenze. Die Methode muss für diesen Sonderfall erweitert werden.
Es bietet sich nun noch an, das Ergebnis mit der Berechnung über die entsprechende Methode aus dem Package java.lang.Math zu vergleichen.
Aufgabe 5
Für viele Zwecke in der Mathematik oder der Kryptographie ist es notwendig Zahlen in ihre Primfaktoren zu zerlegen. Dazu bietet sich folgendes Verfahren an:
In einer Zählschleife wird wiederholt von 2 (kleinster Primfaktor) bis n (Zahl) gezählt, wobei bei jedem Durchlauf überprüft wird, ob die Zählvariable ganzzahliger Teiler der Zahl ist (Modulofunktion: %). Ist dies der Fall, ist ein neuer Primfaktor gefunden und wird als Teil des Produkts der Primzahlen auf der Konsole ausgegeben. Die ganze Schleife wird daraufhin "zurückgesetzt", indem n durch n/Primfaktor ersetzt wird und der Zähler erneut bei 2 beginnt. (Die Zählvariable muss dabei auf 1 (!) gesetzt werden, da am Ende der Schleife diese ja um 1 erhöht wird.). Hinweis: Um eine formal saubere Ausgabe zu erhalten, muss der Faktor 1 als Teil des Produkts verwendet werden.
Erstelle eine Methode primfaktorZerlegung, die nach Übergabe einer Zahl die Zerlegung in ihre Primfaktoren anzeigt.
Aufgabe 6
Die Collatz-Vermutung (auch bekannt als 3n+1-Vermutung) ist eine mathematisches Problem, für das bis heute kein Beweis gefunden werden konnte. Es handelt sich um eine Zahlenreihe, für die folgende Bildungsregel gilt:
Ist die aktuelle Zahl gerade, wird sie durch 2 geteilt, ist sie ungerade, wird sie mit 3 multipliziert und anschließend 1 hinzugezählt.
Die Vermutung lautet, dass bei jeder beliebigen Zahl, diese Reihe schließlich bei 1 endet bzw. in der Wiederholung der Folge 1 - 4 - 2 - 1. Es wurde bisher kein Gegenbeispiel gefunden, aber mathematisch bewiesen werden konnte die Vermutung noch nicht. Erstelle nun eine Methode collatz(int n), die für eine Zahl n ausgibt, in wievielen Schritten die Reihe bei 1 endet.
Erweiterung: Es soll ermittelt werden, bei welcher Zahl innerhalb eines Bereichs von 0 bis n diese Reihe am längsten ist.
Vorlesungausschnitt, in dem die Collatz-Vermutung zur Einführung in JAVA benutzt wird:
Methoden mit Rückgabewert
Häufig verwenden wir eine Methode so, dass sie uns einen Wert zurückgibt, den wir für das weitere Vorgehen nutzen. Eine solche Methode enthält als Ergebnistyp den Datentyp des Rückgabewertes. Beispiel:
//Methode mit Rückgabewert private boolean passwortschutz(String p){ if(p.equals("admin")){return true;} else {System.out.println("Sie haben keine Zugangsberechtigung!"); return false;} }
Diese Methode hat den Ergebnistyp boolean (gibt also als Wert true oder false zurück). Im Rumpf wird überprüft, ob das eingegebene Passwort mit dem hinterlegten ("admin") übereinstimmt. Das Schlüsselwort return bedeutet, dass die Methode hier beendet wird und der berechnete Wert an den Rufer zurückgegeben wird. Eine Methode kann mit return nur einen einzigen Wert zurückgeben. Wir haben Methoden mit Rückgabewert bereits mehrfach kennengelernt. Immer wenn wir z.B. auf eine Methode aus dem Package java.lang.Math zurückgreifen, rufen wir eine Methode auf, die uns einen Wert zurückliefert. Wir vergeben sozusagen den Auftrag für die Berechnung an eine andere Methode. In der Anwendung sieht das dann folgendermaßen aus:
//Methode mit Rückgabewert in der Anwendung public void einzahlen(int betrag, String p){ if(passwortschutz(p)){kontostand=kontostand+betrag;}; } public void auszahlen(int betrag, String p){ if(passwortschutz(p)){kontostand=kontostand-betrag;}; }
Bildhaft können wir uns eine solche Methode mit Rückgabewert vorstellen wie eine Frage nach dem Preis eines Einkaufs in einem Laden. Wir richten eine Anfrage an die Verkäuferin ("Was macht das?") und bekommen das Ergebnis ihrer Berechnung zurückgeliefert. Dieser Gesamtpreis ist das Ergebnis einer einfachen Addition der Warenpreise, die jedesmal erfolgt, wenn ein Kunde sich nach dem zu zahlenden Betrag erkundigt.
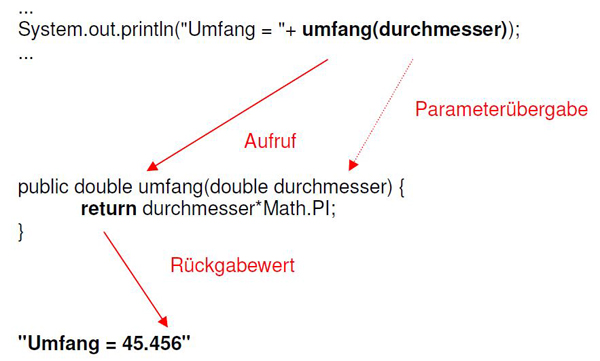
Hier noch einmal graphisch dargestellt die Arbeitweise einer Methode mit Rückgabewert am Beispiel der Berechnung und Ausgabe des Umfangs eines Kreises:
Aufgabe 7
Für diese Aufgabe sind vier Methoden zu erstellen. Eine Methode winkelfunktionen(double x), die für einen beliebigen Eingabewert (x>=0) die drei Winkelfunktionen sin, cos und tan ausgibt. Für die Ermittlung der drei Winkelfunktionen soll jeweils eine eigene Methode mit Rückgabewert erstellt werden, die auf die entsprechende Funktion aus java.lang.Math zurückgreift. Beachte, dass tan x nicht definiert ist, wenn cos x=0 !
Der eingegebene Wert in Grad muss mittels der Methode Math.toRadians(double x) in das Bogenmaß umgerechnet werden.
Um Berechnungsungenauigkeiten aufzufangen, soll folgende Methode eingesetzt werden, um die Ergebnisse auf 8 Stellen zu runden:
private double runden(double wert, int stellen) { return Math.round(wert * Math.pow(10, stellen)) / Math.pow(10, stellen); }
Natürlich lässt sich das Problem einfacher lösen, indem man die entsprechenden Funktionen gleich in der Methode winkelfunktionen (double x) aufruft. Es soll jedoch hier das Prinzip der Dekomposition näher erläutert werden. Der Begriff beschreibt einen Prozess in der Programmierung, bei dem ein komplexes Problem oder System in kleinere Einheiten zerlegt wird, die leichter zu erfassen, zu verstehen, zu programmieren und damit auch zu modifizieren sind. Zudem erhöht sich dadurch die Möglichkeit der Wiederverwendbarkeit von Programmteilen.
Vergegenwärtige dir nach Abschluss der Aufgabe das Zusammenspiel der verschiedenen Methoden.
Aufgabe 8
In einer Klasse Kreistabelle sollen drei Methoden erstellt werden: Die Methode kreistabelleAnzeigen() gibt für Radien von 5 bis 100 in 5er-Schritten den jeweilgen Umfang und Flächeninhalt aus. Die Berechnung von Umfang und Flächeninhalt wird in zwei weitere Methoden ausgelagert.
Getter- und Setter-Methoden
Eine Unterart der Methoden mit Rückgabewert sind sogenannte Getter- und Setter-Methoden. Will man von außen auf private gesetzte Attribute zugreifen, ist dies nur indirekt möglich. Wir nutzen dazu Methoden, die das betreffende Objekt veranlassen, Werte zurückzugeben bzw. zu verändern. Zur Rückgabe von Werten nutzt man sogenannte sondierende Methoden oder Getter-Methoden. Üblicherweise verwendet man als Namen für eine derartige Methode den Bezeichner getAttributname.
Soll der Benutzer auch schreibenden Zugriff auf die Attribute haben, dann erstellt man sogenannte Setter-Methoden, die von außen einen Wert übernehmen und dem auf private gesetzten Attribut zuweisen. Als Bezeichner verwendet man analog zu den Getter-Methoden setAttributname. Beispiele:
public String getName(){ return name; } public String getVorname(){ return vorname; } public String getKontonr(){ return kontonr; } public int getKontostand(){ return kontostand; } public void setKontostand(int neuerKontostand, String p){ if(passwortschutz(p)){kontostand=neuerKontostand;}; }
Die Stärke dieser Vorgehensweise wird bei der letzten Methode deutlich. Während ein direkter Zugriff auf die Attribute der Manipulation von außen Tür und Tor öffnen würde, kann dem durch die Anwendung eines Passwortschutzes innerhalb der Setter-Methode ein Riegel vorgeschoben werden.
Aufgabe 9
Ergänze die Klasse Auto aus Aufgabe 3 um eine Methode getTankinhalt(), die den aktuellen Tankinhalt zurückgibt und sicherstellt, dass nicht mit leerem Tank gefahren wird, bzw. bei einem Tankinhalt von weniger als 10 Litern zum Tanken auffordert.
Aufgabe 10
Erstelle eine Klasse Rechteck mit den Attributen laenge und breite. Neben dem entsprechenden Konstruktor enthält die Klasse Getter- und Setter-Methoden für die beiden Werte. In den Setter-Methoden soll zusätzlich sichergestellt werden, dass die Kantenlänge des Rechtecks den Wert 100 nicht überschreitet. Für den Fall einer Überschreitung wir der Hinweis auf einen unzulässigen Wert ausgegeben. Zusätzlich soll zum Testen eine Methode zur Ausgabe der Werte für laenge und breite angelegt werden.