Computerdenken
Am Ende des Kapitels solltest du
- wissen, was man unter einer Modellierung versteht,
- einfache geometrische Figuren modellieren können,
- wissen, wie ein Computer Farben darstellt,
- Anweisungsfolgen für die Darstellung einfacher geometrischer Muster angeben können.
Grob gesagt befasst sich die Informatik mit der Frage, wie man Probleme aus der realen Welt mit Hilfe elektronischer Datenverarbeitung lösen kann. Egal, ob ich eine email schreibe und versende, am Smartphone Musik höre oder meinen Standort anzeigen lasse, eine Anfrage an eine Suchmaschine richte, mir die Zeit mit einer Spielkonsole vertreibe oder eine Wettervorhersage abrufe, immer liegt dem Vorgang eine Modellierung und Digitalisierung eines Problems zugrunde. Der Computer (von lat. computare - berechnen) muss das Problem in einer Form mitgeteilt bekommen, die es ihm ermöglicht, die Lösung zu berechnen. Wenn wir also einen Computer programmieren, sagen wir ihm, wie er die Lösung zu berechnen hat. Dazu müssen wir unser Problem in eine mathematische Form bringen. Vieles lässt sich mit einfacher Schulmathematik ausdrücken, komplizierte Probleme verlangen aber erwartungsgemäß auch kompliziertere Mathematik. Doch die werden wir den Profis überlassen. Steigen wir mit einem Problem ein, das wir mit den Geometriekenntnissen aus der Unterstufe lösen können.
Problemstellung: Wir wollen auf dem Bildschirm geometrische Figuren darstellen.
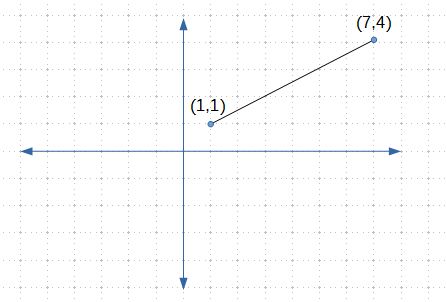
Beginnen wir mit einer einfachen Linie. Sie entsteht aus der Verbindung von zwei Punkten in einem cartesischen Koordinatensystem, das wir auf ein Blatt kariertes Papier gezeichnet haben.
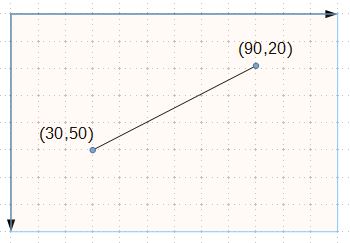
Wir stehen nun vor einem ersten kleinen Modellierungsproblem. Auf einem Computerbildschirm müssen wir einen Fixpunkt für unser Koordinatensystem festlegen. Es ist dies die linke obere Ecke des Bildschirms. Die Einheit unseres Koordinatensystem ist bereits vorgegeben. Es sind dies die einzelnen Bildpunkte (Pixel) unseres Bildschirmfensters. Aus diesem Grund sieht nun die Darstellung unserer Linie etwas anders aus:
In diesem Beispiel ist nun gleichzeitig die Größe der Zeichenfläche markiert. Die geometrische Darstellung der Figur ist nun ungeeignet für die Umsetzung einer Anweisung in einem Computerprogramm. Wir können beispielsweise die Größe der Zeichenfläche durch die Angabe von Breite und Höhe festlegen:
Größe (Breite, Höhe), d.h. in unserem Beispiel Größe(120, 80) oder mit dem englischen Begriff size(120, 80)
Diese Anweisung bedeutet für den Computer: Erstelle eine Zeichenfläche der Breite 120px und der Höhe 80px.
Entsprechend verfahren wir mit der Linie. Wir legen die Koordinaten des Startpunktes und des Endpunktes fest:
Linie (xPosition A, yPosition A, xPosition B, yPosition B), d.h. in unserem Beispiel Linie(30, 50, 90, 20) oder mit dem englischen Begriff line(30, 50, 90, 20).
Diese Anweisung bedeutet für den Computer: Zeichne eine Linie vom Punkt (30, 50) zum Punkt(90, 20).
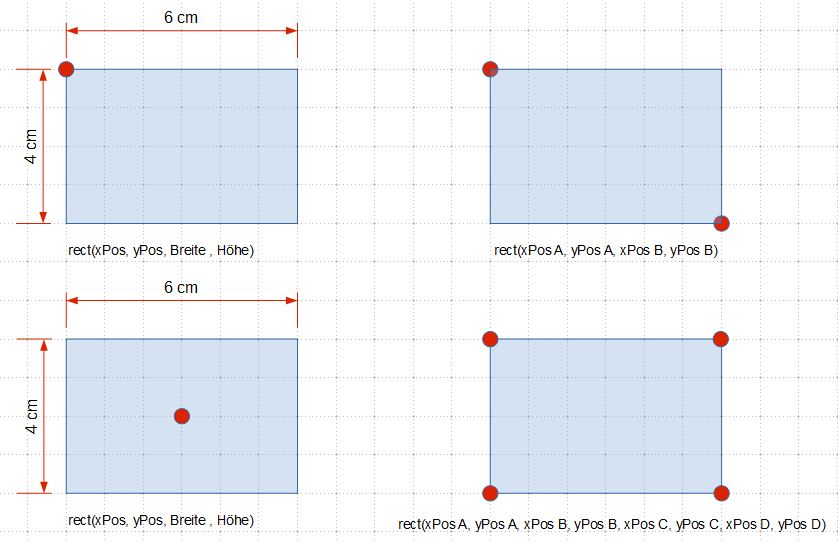
Aufgabe
Gib nach obiger Vorgehensweise vier Möglichkeiten an um ein Rechteck zu modellieren.
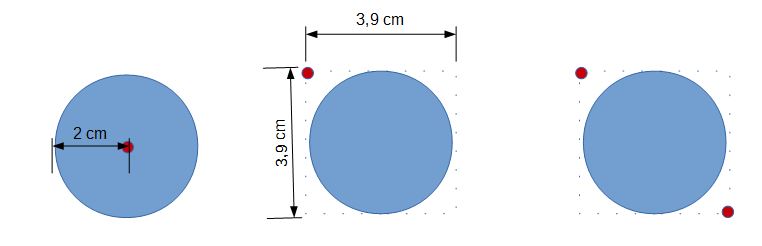
Aufgabe
Gib nach obiger Vorgehensweise zwei Möglichkeiten an um eine Ellipse zu modellieren.
Problemstellung: Wir wollen auf dem Bildschirm Farben darstellen.
Wenn wir unsere Darstellungsmöglichkeiten erweitern wollen, müssen wir einen Weg finden, unseren geometrischen Figuren Farbeigenschaften zu verleihen, d.h. unsere Umrisslinien sollen farbig werden und unsere Figuren sollen eine Füllfarbe erhalten. Dazu müssen wir einen Weg finden die praktisch unbegrenzte Zahl von Farben in ein digitales Schema zu bringen. Um eine Farbe zu definieren, macht man sich die Tatsache zunutze, dass jede Farbe als Kombination bestimmter Anteile von Rot, Grün und Blau gesehen werden kann. Entsprechend wird für den Computer dieser Anteil durch eine Zahl zwischen 0 und 255 angegeben (= 8 bit bzw. 1 byte). Wir benötigen also für diese Information insgesamt 24 bit. Beispiel: Die Farbe "weiß" hat die Kombination R:255 - G:255 - B:255.
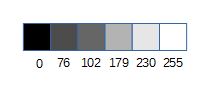
Relativ einfach ist die Darstellung von Grauwerten. Da jeder Grauwert den jeweils gleichen Anteil von Rot, Grün und Blau hat, müssen wir nur eine Zahl zwischen 0 und 255 angeben:
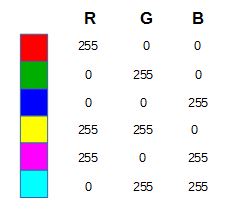
Bei den anderen Farben müssen wir dagegen alle drei Werte der jeweiligen Farbe angeben:
Man kann übrigens noch einen vierten Wert hinzufügen, der für die Transparenz der Farbe, den sogenannten Alphawert, steht. Dabei bedeutet 0 "völlig transparent" und 255 "völlig opaque", d.h. undurchlässig.
Wenn wir nun dem Computer die Anweisung geben wollen, eine blaue Linie zu zeichnen, dann müssen wir ihm zuerst sagen, dass er für den Strich eine blaue Farbe wählen soll und ihm anschließend die Werte für die zu zeichnende Linie mitteilen:
Strich (Rot, Grün, Blau), d.h. in unserem Beispiel Strich (0, 0, 255) oder mit dem englischen Begriff stroke(0, 0, 255)
Analog gehen wir beim Einfärben eines Rechtecks vor. Bevor wie das Rechteck zeichnen legen wir die Füllfarbe (z.B. rot) fest:
Füllung (Rot, Grün, Blau), d.h. in unserem Beispiel Füllung (255, 0, 0) oder mit dem englischen Begriff fill(255, 0, 0)
Zusätzlich können wir auch noch eine Hintergrundfarbe festlegen (z.B. gelb):
Hintergrund (Rot, Grün, Blau), d.h. in unserem Beispiel Hintergrund (255, 255, 0) oder mit dem englischen Begriff background(255, 255, 0)
Damit haben wir nun einige Elemente einer Sprache, die geeignet ist, einem Computer Anweisungen zu geben, da sie die Voraussetzung der Mathematisierung und Digitalisierung der Daten erfüllt. Mit diesen Elementen können wir auch die Anweisungsfolge für die Darstellung des folgenden Beispiels angeben:
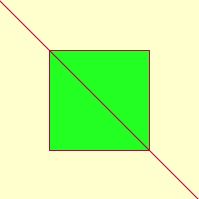 |
size(200,200); background(255,255,204); stroke(184,0,71); fill(35,255,34); rect(50,50,100,100); line(0,0,200,200); |
Wie in den meisten Programmiersprachen üblich, schließen wir jede Anweisung mit einem Semikolon ab.
Aufgabe
Warum ist die Umrisslinie des Rechtecks rot? Ändere die Anweisungen so ab, dass diese Umrisslinie blau wird, ohne dabei aber die Farbe der Diagonale zu ändern.