Bedingungen in Processing

Am Ende des Kapitels solltest du

• wissen, was eine Bedingung ist,
• boolsche Operatoren kennen,
• wissen, wie Bedingungen ausgewertet werden,
• logische Operatoren einsetzen können,
• wissen, wie if-, if-else- und else if - Anweisungen funktionieren,
• in der Lage sein, ein Ablaufdiagramm zu lesen.

Unter einer Bedingung versteht man einen beliebigen Ausdruck, dessen Auswertung einen Wahrheitswert (true oder false) liefert. Am häufigsten handelt es sich dabei um Vergleiche:

Ausdruck	Bedeutung
(x == 0)	x ist gleich 0 (Gleichheitsoperator)
(x != 0)	x ist ungleich 0 (Ungleichheitsoperator)
(x > 0), (x < 0)	x größer 0, x kleiner 0
(x >= 0), (x <= 0)	x größer oder gleich 0, x kleiner oder gleich 0

Im Laufe der Zeit werden wir noch weitere Möglichkeiten für Ausdrücke kennen lernen, deren Auswertung true oder false ergibt. Wir haben also hier einen Wert vom Typ boolean. Processing kennt nun verschiedene Kontrollstrukturen, die diese Ausdrücke nutzen.

Die if-Anweisung

Wir kennen diese Struktur bereits vom Programmieren mit Robot Karol oder Scratch. Eine Anweisung wird nur ausgeführt, wenn die Auswertung der Bedingung den Wert true ergibt. In Processing sieht diese Anweisung folgendermaßen aus:

if(Ausdruck){Anweisung}

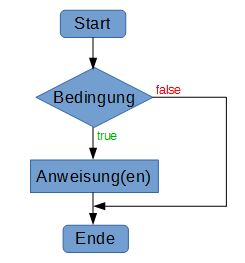
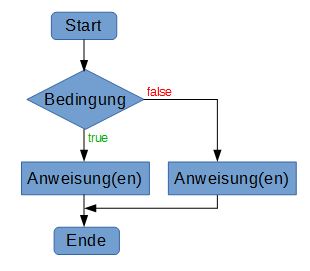
Wir können diese Struktur auch in Form eines Ablaufdiagramms darstellen:

Sehen wir uns die Bedingung gleich in Aktion an:

int xPos = 0;
int v = 3;
 
void setup(){
  size(600,400);
}
 
void draw(){
  background(0);
  stroke(255, 0, 0);
  strokeWeight(10);
  xPos = xPos + v;
 
  //Bedingung
  if(xPos > width){
    xPos = 0;};
 
  point(xPos, height/2);
}

Die Anweisung xPos = xPos + v; sorgt dafür, dass sich der Punkt von links nach rechts bewegt. Bei jeder Aktualisierung durch draw() wird in der if-Anweisung überprüft, ob der Punkt bereits den rechten Rand überschritten hat (if(xPos > width)). Ist dies der Fall, wird die entsprechende Anweisung ausgeführt und der Punkt wieder an den linken Rand gesetzt (xPos=0).

Aufgabe 1

a) Ändere das obige Programm so ab, dass der Punkt alle 150px seine Farbe ändert.

Lösungsvorschlag anzeigen

Lösungsvorschlag verstecken

int xPos = 0;
int v = 3;
 
void setup(){
  size(600,400);
}
 
void draw(){
  background(0);
  stroke(255, 0, 0);
  strokeWeight(10);
  xPos = xPos + v;
 
  //Bedingung
  if(xPos > width){
    xPos = 0;};
 
 //Änderung der Farbe des Punktes
 if(xPos>150){stroke(0,255,0);};
 if(xPos>300){stroke(0,0,255);};
 if(xPos>450){stroke(255,255,0);};
 
  point(xPos, height/2);
}

b) Ändere das Programm so ab, dass der Punkt sich von links oben nach rechts unten bewegt und zunehmend größer wird. (Wiederholung von Variablen)

Lösungsvorschlag anzeigen

Lösungsvorschlag verstecken

float xPos = 0;
float yPos = 0;
//Geschwindigkeit angepasst an die Fenstergröße
float v1 = 3;
float v2 = 2;
//Größe des Punktes
float g = 10;
 
void setup(){
  size(600,400);
}
 
void draw(){
  background(0);
  stroke(255, 0, 0);
  strokeWeight(g);
  xPos = xPos + v1;
  yPos = yPos + v2;
 
  //Bedingung
  if(xPos > width){
    xPos = 0;
    yPos = 0;};
 
 //Änderung der Farbe des Punktes
 if(xPos>150){stroke(0,255,0);};
 if(xPos>300){stroke(0,0,255);};
 if(xPos>450){stroke(255,255,0);};
 
  point(xPos, yPos);
  //Vergrößerung des Punktes bei jeder Aktualisierung
  g = g+ 0.01;
}

Aufgabe 2

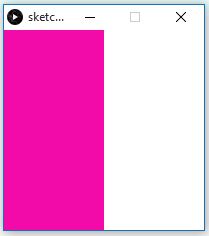
Erstelle ein Programm, das bei einem Mausklick in die linke Seite des Zeichenfensters, diese mit einer zufällig gewählten Farbe einfärbt und bei einem Klick in die rechte Hälfte das Zeichenfenster wieder weiß färbt. (Wiederholung von Systemvariablen)

Lösungsvorschlag anzeigen

Lösungsvorschlag verstecken

void setup(){
  size(200,200);
}
 
void draw(){
 
}
 
void mousePressed(){
  background(255);
  if(mouseX<width/2){
    noStroke();
    fill(random(256), random(256), random(256));
    rect(0,0,width/2, height);
  }
}

Aufgabe 3

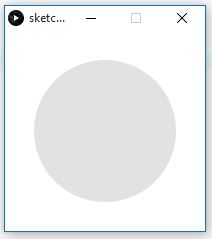
Ein mittig platzierter Kreis wird stetig größer, bis er den Rand des Fensters erreicht, dann beginnt er wieder als ein kleiner Kreis zu wachsen. Gleichzeitig soll der Kreis jede Sekunde seine Farbe um eine Graustufe verändern, so dass er bei weiß beginnend sich mit der Zeit schwarz färbt. Hat er die Farbe Schwarz erreicht, soll er wieder bei weiß beginnen. (Hinweis: Die Veränderung läßt sich über eine Zählvariable steuern. Wir wissen, dass die draw()-Methode das Zeichenfenster 60 mal pro Sekunde aktualisiert. Das können wir uns hier zunutze machen.)

Lösungsvorschlag anzeigen

Lösungsvorschlag verstecken

float h = 0;
float b = 0;
int g = 255;
int count = 0;
 
void setup(){
size(200,200);
}
 
void draw(){
background(255);
noStroke();
fill(g);
ellipse(100, 100, h, b);
h=h+2;
b=b+2;
if(count==60){g=g-1; count=0;};
if(h>200){h=0; b=0;};
if(g==0){g=255;};
count++;
}

Aufgabe 4

a) Ein Ball soll sich auf der Zeichenfläche von links nach rechts bewegen und dann jeweils von der Seite abprallen und sich wieder zurückbewegen. Bei jedem Abprall ändert er zudem seine Farbe.

Lösungsvorschlag anzeigen

Lösungsvorschlag verstecken

//Startpunkt x=10 statt x=0, da sonst die zweite Bedingung den Start blockiert
float x=10;
//Geschwindigkeit
float a=5;
 
void setup(){
  size(800, 400);
  //Farbe des Kreises bei Programmstart
  fill(255, 255,0);
}
 
void draw(){
  background(0);
  //Abprallen von der rechten Kante. Richtungswechsel durch Vorzeichenumkehr bei der Geschwindigkeit
  if(x>width-10){a=-a; fill(255, 0, 0);};
  //Abprallen von der linken Kante
  if(x<10){a=-a; fill(255, 255, 0);};
 
  ellipse(x, 100, 20, 20);
  x=x+a;
  }

b) Der Ball soll sich nun beliebig auf der Zeichenfläche bewegen und jeweils vom Rand abprallen. (Auf die Farbänderung kann nun verzichtet werden.)

Lösungsvorschlag anzeigen

Lösungsvorschlag verstecken

//Startposition des Balles
float x = 100;
float y = 100;
//Geschwindigkeit des Balles in x- bzw. y-Richtung
float vX = 2;
float vY = 6;
 
void setup() {
  size(300,300);
}
 
void draw() {
  background(0);
 
//Bewegung des Balles
  x = x + vX;
  y = y + vY;
 
//Überprüfen, ob der Ball abprallt
  if ((x > width-10) || (x < 10)) {
    vX = -vX;
  }
  if ((y > height-10) || (y < 10)) {
    vY = -vY;
  }
 
//Ball zeichnen
  fill(255);
  ellipse(x,y,20,20);
}

Komplexere Bedingungen entstehen durch die Verknüpfung mehrerer Vergleiche mittels logischer Operatoren:

Logischer Operator	Bedeutung	Beispiel
&&	logisches UND	(x>5) && (x<9)
||	logisches ODER	(x<5) || (x>9)
!	logisches NICHT	!(x==0)

In folgendem Programm ändert der Punkt in einem bestimmten Bereich (200 < x <400) seine Größe:

int xPos = 0;
int v = 3;
 
void setup(){
  size(600,400);
}
 
void draw(){
  background(0);
  stroke(255, 0, 0);
  strokeWeight(10);
  xPos = xPos + v;
 
  //Bedingung
  if(xPos > width){
    xPos = 0;};
 
  //Größenänderung 
  if(xPos>200 && xPos<400){
    strokeWeight(20);
  }
 
  point(xPos, height/2);
}

Aufgabe 5

Erweitere das Programm aus Aufgabe 2 so, dass mit einem entsprechenden Mausklick in das Feld die Farbe eines der vier Quadranten geändert wird.

Lösungsvorschlag anzeigen

Lösungsvorschlag verstecken

void setup(){
  size(200,200);
  background(255);
}
 
void draw(){
 
}
 
void mousePressed(){
 
  noStroke();
 
 
  if(mouseX<width/2 && mouseY<height/2){  
     fill(random(256), random(256), random(256));    
     rect(0,0,width/2, height/2);
  }
 
  if(mouseX>width/2 && mouseY<height/2){ 
     fill(random(256), random(256), random(256));     
     rect(100,0,width/2, height/2);
  }
 
  if(mouseX<width/2 && mouseY>height/2){   
     fill(random(256), random(256), random(256));     
     rect(0,100,width/2, height/2);
  }
 
 if(mouseX>width/2 && mouseY>height/2){   
     fill(random(256), random(256), random(256));    
     rect(100,100,width/2, height/2);
  }  
}

Die else-Anweisung

Wollen wir auch für den Fall, dass die angegebene Bedingung nicht eintritt, angeben, was passieren soll, müssen wir die Bedingung um einen else-Teil erweitern.

if(Ausdruck){Anweisung, wenn der Ausdruck wahr ergibt}
else {Anweisung, wenn der Ausdruck falsch ergibt}

Auch hier ist wieder ein Ablaufdiagramm von Vorteil für das Verständnis:

Ist die Bedingung im if-Zweig erfüllt, dann wird die zugehörige Anweisung ausgeführt. Ist dies nicht der Fall, so wird die Anweisung aus dem else-Zweig ausgeführt.

Beispiel:

void setup(){
  size(200, 200);
 
}
 
void draw(){
 background(0);
 noStroke();
 ellipse(width/2, height/2, mouseX, mouseY);
 if(mouseX>100){fill(255, 0, 0);}
 else {fill(255, 255, 0);};
}

In diesem Beispiel ist die Farbe der Ellipse von ihrer Größe abhängig. Ist der Parameterwert für die Breite kleiner als 100, ist die Ellipse gelb gefärbt, in allen anderen Fällen rot.

Aufgabe 6

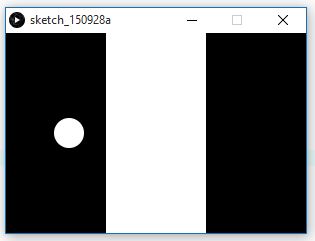
In folgendem Feld bewegt sich ein Kreis fortlaufend von links nach rechts. Solange er im schwarzen Feld ist, ist er weiß, läuft er durch das weiße Feld, ist er schwarz. Löse das Problem mit einer if-else-Anweisung.

Lösungsvorschlag anzeigen

Lösungsvorschlag verstecken

float x=0;
 
void setup(){
  size(300, 200);
 
}
 
void draw(){
  background(255); 
  noStroke();
  fill(0);
  rect(0, 0, 100,200);
  rect(200, 0, 100, 200);
 
  if(x>100 && x<200){fill(0);}
  else {fill(255);};
 
  ellipse(x, 100, 30, 30);
  x=x+1; 
  if(x>300){x=0;};
}

Aufgabe 7

Ein gieriger Pacman jagt hinter einem unschuldigen Opfer her und öffnet und schließt dabei sein Maul. Sind die beiden am rechten Rand angekommen, geht die Jagd von neuem los. Dabei soll Pacman seinem Opfer auf der Strecke immer näher kommen ohne es zu erwischen. Erscheinen die beiden am linken Rand wieder, hat das Opfer seinen alten Vorsprung wieder.

[ www.youtube.com is not an authorized iframe site ]

Lösungsvorschlag anzeigen

Lösungsvorschlag verstecken

float x = 0;
float x1 = 110;
//Geschwindigkeit Pacman
float v = 3;
//Geschwindigkeit Opfer
float v1 = 2.85;
int count = 0;
 
void setup(){
  size(1000, 300);
  background(0);
}
 
void draw(){
  background(0);
 
  //Der gierige Pacman
  fill(255, 255,0);
  ellipse(x, 150, 100, 100);
 
  //Pacmans Auge
  fill(0);
  ellipse(x+5, 120, 15, 15);
 
  //Das kleine rote Opfer
  fill(255, 0, 0);
  ellipse(x1, 150, 10, 10);
 
  //Wechsel zwischen geöffneten und geschlossenem Maul
  //Variable count steuert Frequenz der Maulöffnung
  if(count < 30){stroke(0); fill(0);} else {noStroke(); noFill();}
 
  //Pacmans Maul
  triangle(x-5, 150, x+50, 120, x+50, 180);
 
  //Steuerung der Geschwindigkeit von Pacman und seinem Opfer
  x = x + v;
  x1 = x1 + v1;
 
  //Aktualisierung des Zählers
  count++;
 
  //Rückstellung des Zählers
  if(count>60){count = 0;};
 
  //Rückkehr von Pacman zum Startpunkt; Opfer erhält alten Vorsprung
  if(x>width){x = 0; x1 = x+110;};
 
}

Die else-if - Anweisung

Stehen mehrere Alternativen zur Verfügung, die jeweils unterschiedliche Anweisungen nach sich ziehen, können wir eine else-if - Struktur nutzen:

if (Ausdruck 1){Anweisung 1}
else if (Ausdruck 2){Anweisung 2}
          .
          .
          .
else if (Ausdruck n){Anweisung n}
else {Anweisung_else}

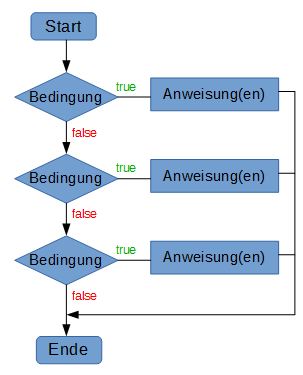
Das Ablaufdiagramm für die Struktur sieht folgendermaßen aus:

In der angegebenen Reihenfolge wird ein Ausdruck nach dem anderen abgearbeitet. Bei der ersten Bedingung, die true ist, wird die zugehörige Anweisung bzw. der zugehörige Anweisungsblock ausgeführt und die Mehrfachauswahl abgebrochen. Der letzte else-Zweig ist optional. Hier können alle anderen Fälle behandelt werden, die nicht explizit aufgeführt wurden. Ist dies nicht notwendig, so kann der else-Zweig entfallen.

Beispiel:

void setup(){
  size(600,200);
  //Aktualisierungsrate 2 frames/s um den Effekt beobachten zu können
  frameRate(2);
}
 
void draw(){
  background(0);
  float x=random(width);
 
  if(x<100){fill(255, 0, 0);}
  else if(x<200){fill(255, 255, 0);}
  else if(x<300){fill(255, 0, 255);}
  else if(x<400){fill(0, 255, 255);}
  else {fill(0, 255, 0);};
 
  ellipse(x, 100, 20, 20);
}

Der Kreis wird auf eine zufällige x-Position auf der Zeichenfläche gesetzt und erhält abhängig von der Position eine bestimmte Farbe

Aufgabe 8

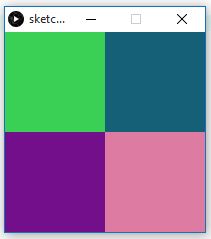
Auf der Zeichenfläche, das wir uns in vier Quadranten eingeteilt vorstellen, bewegen wir mit der Maus einen kleinen Kreis. Je nachdem, in welchem Quadranten sich der Kreis gerade befindet, nimmt er eine andere Farbe an. Löse das Problem mit einer else-if - Struktur.

Lösungsvorschlag anzeigen

Lösungsvorschlag verstecken

void setup(){
  size(400,400);
 
}
 
void draw(){
  background(0);
  float x=mouseX;
  float y=mouseY;
  ellipse(mouseX, mouseY, 20, 20);
 
  if(x<200 && y<200){fill(255, 0, 0);}
  else if(x>200 && y<200){fill(255, 255, 0);}
  else if(x<200 && y>200){fill(255, 0, 255);}
  else if(x>200 && y>200){fill(0, 255, 255);};
 
}

Projekt

Processing eignet sich gut um physikalische Zusammenhänge zu visualisieren. In diesem kleinen Projekt sollen der freie Fall, das Rollen einer Kugel auf einer schiefen Ebene und eine Wurfparabel simuliert werden. Die bisher kennengelernten Elemente der Sprache reichen dazu aus. Einzig Winkelfunktionen kommen noch hinzu: In Processing müssen Winkel im Bogenmaß angegeben werden. Dies können wir mittels der Funktion radians erreichen (float alpha = radians(Winkel in Grad)). Die Winkelfunktionen nutzen wir intuitiv: sin(alpha), cos(alpha) und tan(alpha). Hilfreich ist zudem die Funktion pow() zum Quadrieren von Zahlen.

Recherchiere jeweils in einem ersten Schritt die physikalischen Grundlagen. Wir suchen jeweils die Formel um x- bzw. y-Wert der aktuellen Position der Kugel bei jeder Aktualisierung der Zeichenfläche zu ermitteln.

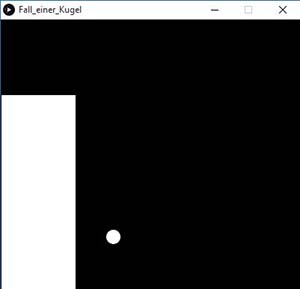
Teil 1: Freier Fall

Eine schwere Kugel rollt mit einer Anfangsgeschwindigkeit v zur Kante und fällt dann zu Boden. Wenn sie dort aufschlägt, rollt sie weiter bis zum rechten Rand und bleibt dann liegen. Um eine realistische Darstellung zu erhalten, muss man mit der Zeitvariable und der Framerate etwas experimentieren.

Lösungsvorschlag anzeigen

Lösungsvorschlag verstecken

//Startpunkt der Kugel
float x = 10;
float y = 90;
//Festlegung der Startgeschwindigkeit
float v = 4;
//Startwert für die Zeitvariable (t>0)
float t = 0.1;
 
void setup(){
 size(400, 600);
frameRate(30);
}
 
void draw(){
  background(0);
  //Zeichnen der Kante
  fill(255);
  rect(0,100,150,500);
 
  //Bewegung der Kugel vor der Kante
  if(x<150){x=x+v; y=90;}
  //Fall der Kugel
  else{
  x=x+v*t;
  y=y+0.5*9.81*t*t;};
 
  //Auftreffen der Kugel am Boden und Weiterrollen
   if(y>height-10){x=x+v; y=height-10;};
   //Halten der Kugel an der Wand
   if(x>width-20){x=width-10; y=height-10;};
  //Zeichnen der Kugel
  fill(255);
  ellipse(x,y,20,20);
 
  //Aktualisierung der Zeitvariable
  t=t+0.05;  
}

Teil 2: Schiefe Ebene

Eine Kugel rollt eine Schiefe Ebene hinab. Als Erweiterung kann man die Kugel zum rechten Rand weiterrollen lassen. Zu diesem Zweck benötigt man die Geschwindigkeit der Kugel am Ende der schiefen Ebene.

Lösungsvorschlag anzeigen

Lösungsvorschlag verstecken

//Position des Kreises
float y;
float x;
//Neigungswinkel der schiefen Ebene
float alpha = radians(10);
//Die Position wird 60 mal pro Sekunde aktualisiert, also t = 1/60
float t = 0.167;
 
void setup(){
 size(1800, 800);
 background(0);
}
 
 
void draw(){
 
//Hintergrund um den Nachzieheffekt zu vermeiden
background(0);
 
//Schiefe Ebene
triangle(0, height-400, 0, height, (height-400)/sin(alpha),height);
fill(255);
 
 
//Positionsveränderung
//Teiler 60 um die Darstellung flüssiger zu machen
y = (y + 0.5 * 9.81 * pow(t,2))/60;
x = y/tan(alpha);
 
//Zeichnen der Kugel
ellipse(x,y+(height-420),40,40);  
 
//Aktualisierung der Zeitkomponente
t = t + 0.167;
}

Teil 3: Wurfparabel

Das Programm zeigt die Flugbahn eines Projektils bei verschiedenen Abschusswinkeln und Abwurfhöhen an.

Lösungsvorschlag anzeigen

Lösungsvorschlag verstecken

float alpha = radians(30);
 
float x=0;
float y;
 
float v=10;
 
 
void setup(){
  size(1200, 800);
  background(0);
}
 
void draw(){
 
  if(y>height-30){y=height-20; noLoop();};
 
  y = 700 - x*tan(alpha) + (9.81 * pow(x,2))/(2*pow(v*cos(alpha),2))/100;
  stroke(255,0,0);
  strokeWeight(3);
  fill(255);
  point(x,y);
 
  x = x+8;
}